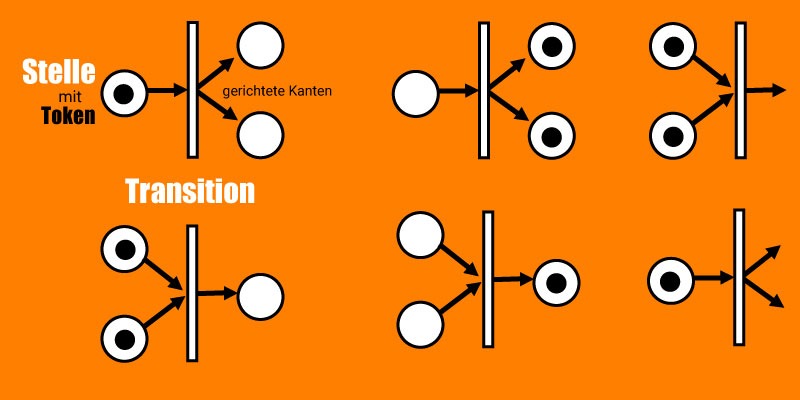
Petri-Netze werden meist verwendet, um technische Prozesse zu modellieren, wie zum Beispiel im Maschinenbau oder der Logistik. Das Modell von Carl Adam Petri wurde seit den 1960er Jahren immer weiter entwickelt. Heutzutage wird häufig mit “Coloured Petri-Nets” (CP-Nets, CPN) modelliert. Ein Petri Netz besteht aus verschiedenen Knoten, die durch Richtungspfeile (gerichtete Kanten) miteinander verbunden werden. Bei den Knoten wird zwischen Stellen und Transitionen unterschieden.
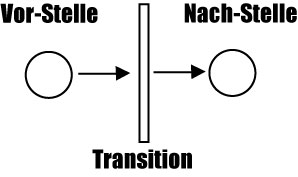 |
Ein Kreis symbolisiert eine Stelle, einen Platz für Daten. Eine Transition beschreibt die Verarbeitung von Daten. Der Übergang wird durch einen Balken dargestellt. Die Kanten führen immer nur von Stellen zu Transitionen oder umgekehrt. |
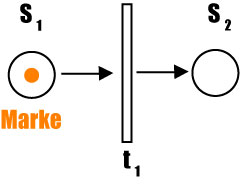 |
Durch Marken, die entlang der Kanten wandern, wird der Prozess beschrieben. Die Transitionen schalten und feuern Marken aus den Stellen in die nachfolgenden Stellen. Solange eine Transition mehr Marken benötigt, als tatsächlich dort liegen, kann sie nicht schalten. |
Feuerungsregeln der Übergänge

| 1 | Wenn auf der Vor-Stelle A eine Marke liegt, feuert die Transition die Marke auf beide Nach-Stellen B und C bis beide mit Marken belegt sind. | A → B ∧ C |
| 2 | Die Marke auf der Vor-Stelle wird entweder über die erste oder über die zweite Transition weitergeleitet. Entweder auf Nach-Stellen B oder C. | A → B ∨ C (exklusiv) |
| 3 | Auf beiden Vor-Stellen A und B liegen Marken. Wenn die und Nach-Stelle C leer ist, feuert entweder die erste oder die zweite Transition. | A ∨ B → C |
| 4 | Erst wenn beide Vor-Stellen A und B mit Marken belegt sind. feuert die Transition eine Marke auf die Nach-Stelle C. | A ∧ B → C |
Einfaches Petri-Netz – Briefsortiermaschine
Bei einfachen Petri-Netzen kann jede Stelle nur mit maximal einer Marke belegt sein. Ein Beispiel aus dem Modul “Einführung in die Informatik der virtuellen Fachhochschule ist eine Briefsortiermaschine. Wirft man einen Brief in einen Briefkasten mit Kartenleser wird der Brief je nach verwendeter Karte in Sack 1 oder Sack 2 einsortiert. Ohne Karte kann kein Brief eingesteckt werden.
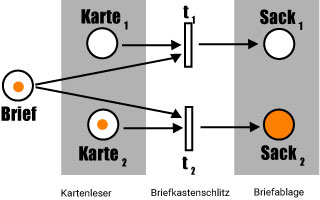
Stellen-Transitions-Netz (nat-Petri-Netz)
Bei komplexeren Petri-Netzen können die Stellen auch mehrere Marken enthalten. Dann notiert man neben dem Stellensymbol die Kapazität ( Anzahl Obergrenze). Jedem Ein- und Ausgang einer Transition wird ein Gewicht zugewiesen, das angibt wie viele Marken beim Schalten verbraucht werden. Hierfür wird der Pfeil beschriftet, der Stelle und Transition verbindet.
Achtung Fachjargon: Ein Petri-Netz ist ein bipartiter Graph, also ein Graph mit zwei andersartigen Knoten. Mathematiker nennen es zwei Mengen S (Stellen) und T (Transitionen) mit einer Relation F. Es ist aber nur ein Petri-Netz wenn die beiden Mengen disjunkt sind und die Vereinigung beider Mengen nicht leer ist. Weiterhin dürfen durch die Relation F nur die Elemente aus den verschiedenen Mengen verknüpft sein und es darf kein Element isoliert sein.